진수, 진법에 대한 이해
컴퓨터는 사람이 계산하는 방식과 다른 원리로 계산을 한다. 일반적으로 사람은 수를 계산할 때 10진수를 사용하는데 손가락의 개수가 8개면 8진수, 16개였으면 16진수가 자연스럽게 사용할 수도 있었을 것이다. 평소에는 10진수 외에는 몰라도 되지만 컴퓨터 공부를 하고 있는 지금 진수와 진법에 대해 조금 더 알아볼 필요가 있다고 생각했다.
진법
0부터 n개의 숫자를 사용하여 수를 표현하는 방법, 0~(n-1)만큼 표현.
진법이란 수를 표기하는 기수법의 하나로 임의의 숫자를 사용하여 수를 표현하는 방법이다. 우리가 일반적으로 사용하는 1부터 9까지의 숫자를 사용하여 수를 나타내는 방법은 10진법이라고 부른다. 현재 프로그래밍에서 많이 사용되고 있는 진법은 2진법, 8진법, 10진법, 16진법이 있다.
**기수법 : 수를 기록하는 방법으로 일반적으로 유한개의 기호(문자, 숫자)를 사용하여 수를 표현하는 방법이며, 오늘날은 주로 십진기수법을 사용하고 있다. (네이버 수학백과)
진수
진법으로 나타내어진 수로 n진법으로 나타낸 수 : n진수.
2진법 : 0부터 2개의 숫자를 사용하여 0~1을 표현
8진법 : 0부터 8개의 숫자를 사용하여 0~7을 표현
10진법 : 0부터 10개의 숫자를 사용하여 0~9를 표현
16진법 : 0부터 16개의 숫자를 사용하여 0~15를 표현
8진법 16진법 왜쓰는가?
최초의 컴퓨터 애니악(ENIAC)은 사람에게 익숙한 10진법을 사용하도록 설계되었다. 하지만 전압을 10단계 나누어 처리하는 데 전기회로의 전압이 불안정했다. 그 후, 1950년에 개발된 에드박(EDVAC)은 2진법으로 전기가 흐르면 1, 흐르지 않으면 0으로 동작하도록 하였다. 매우 안정적인 결과였고 이후부터 컴퓨터는 2진 체계로 설계되었다.
2진법은 데이터를 표현하기 위해 상당히 많은 자리수를 차지한다. 이렇게 많은 자리수는 가독성을 해칠 수 있으며 이러한 단점을 보완하기 위해서 8진법과 16진법이 등장했다. 8진법 하나로 2의3승 자리를 표현할 수 있고, 16진법 하나로 2의4승 자리를 표현할 수 있다. 즉, 2진법보다 자리를 덜 차지하기 때문에 효율이 좋아진다.
8진법을 사용하는 대표적인 예시는 리눅스나 FTP등에서 파일이나 폴더 권한을 표현하기 위해서 많이 사용된다.
16진법을 사용하는 대표적인 예시는 rgb칼라코드, 유니코드 등에서 사용된다.
2진법(binary notation)
2진법은 0과 1, 두 개의 숫자만으로 수를 표현하는 방법이다.
0~1까지 두 개의 숫자를 세다가 더 이상 표현할 수가 없을 때 높은 자릿수를 1 증가시켜 다음수를 표현한다.
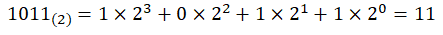
| 2진수 | 10진수 |
| 0 | 0 |
| 1 | 1 |
| 10 (올림발생) | 2 |
| 11 | 3 |
| 100 (올림발생) | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 (올림발생) | 8 |
| 1001 | 9 |
| 1010 | 10 (올림발생) |
8진법(octal notation)
8진법은 0, 1, 2, 3, 4, 5, 6, 7 여덟 개의 숫자로 수를 표현하는 방법이다.
8진수는 2진수를 3자리씩 빠르게 묶어 표현할 수 있어서, 비트 단위까지 신경쓰며 프로그래밍을 하던 초창기 컴퓨터에서 많이 사용했다.
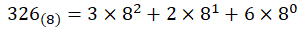
| 2진수 | 8진수 | 10진수 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 10 | 2 | 2 |
| 11 | 3 | 3 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
| 1000 | 10 | 8 |
10진법(decimal notation)
10진법은 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 열 개의 숫자로 수를 표현하는 방법이다.
우리가 일상생활에서 수를 나타낼 때 흔히 사용하는 방법이다.
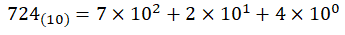
16진법(hexadecimal notation)
16진법은 16개의 기호가 필요하므로 0~9의 숫자만으로는 부족하여 문자 A~F를 추가로 사용한다.
16진수는 특히 컴퓨터 분야에서 1바이트(byte)의 크기를 쉽게 표현할 수 있어서 많이 사용되고 있다.
16진수는 자리수 하나로 0부터 15까지의 숫자를 표현할 수 있다.
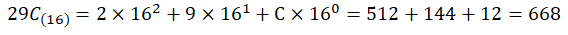
| 2진수 | 8진수 | 10진수 | 16진수 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 10 | 2 | 2 | 2 |
| 11 | 3 | 3 | 3 |
| 100 | 4 | 4 | 4 |
| 101 | 5 | 5 | 5 |
| 110 | 6 | 6 | 6 |
| 111 | 7 | 7 | 7 |
| 1000 | 10 | 8 | 8 |
| 1001 | 11 | 9 | 9 |
| 1010 | 12 | 10 | A |
| 1011 | 13 | 11 | B |
| 1100 | 14 | 12 | C |
| 1101 | 15 | 13 | D |
| 1110 | 16 | 14 | E |
| 1111 | 17 | 15 | F |
| 10000 | 20 | 16 | 10 |
진법변환
10진수를 각 진법으로 변환하는 방법은 아래와 같다.
1) 10진수를 변환하고자 하는 진법의 기수로 나누고, 나머지를 기록한다.
2) 나눈 몫을 다시 변환하고자 하는 진법의 기수로 몫이 가수보다 작아질 때 까지 나누고 나머지를 기록한다.
3) 마지막 몫과 지금까지 기록한 나머지들을 연결하면 해당 진법의 수가 완성된다.
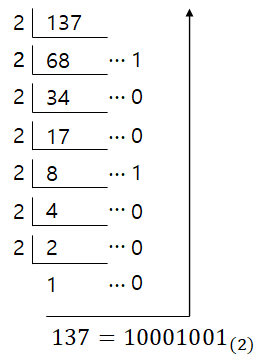
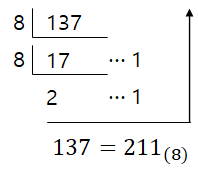

2진수, 8진수, 16진수를 10진수로 변환하는 방법은 위의 진법 설명에 수식을 보며 이해하는 것이 빠르다.
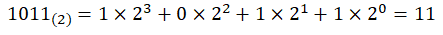
2진수인 1011을 10진수로 변환할 때 1의자리 수 부터 각각 2의 0승, 2의 1승, 2의 2승 ... 2의 n승을 차례대로 곱해주면 된다.
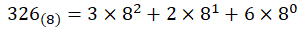
8진수인 326 또한 10진수로 변환할 때 1의자리 수 부터 각각 8의 0승, 8의 1승, 8의 2승 ... 8의 n승을 차례대로 곱해주면 된다.
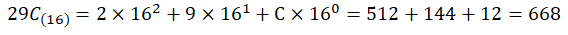
16진수도 2진수, 8진수와 똑같이 1의자리 수 부터 각각 16의 0승, 16의 1승, ..., 16의 n승을 차례대로 곱해준다.
'⭐️ CS & Algorithm > Computer Science' 카테고리의 다른 글
| SPA 이해하기 (0) | 2023.01.25 |
|---|---|
| CORS란 무엇인가? (0) | 2022.08.16 |
| URL 이해하기 (0) | 2022.08.15 |